Definition
The Normal Distribution is one of the most important distributions in the application of statistical methods to business process improvement.
The normal distribution is a bell-shaped curve, symmetric about its mean with the tails extending out to infinity. Its shape and location are fully defined by two parameters: the mean and standard deviation (or variance). The normal distribution is important for two reasons:
1) Many widely used statistical techniques are based on the assumption that the distribution underlying the sample data is normal.
2) The distribution of sample Means from any distribution is well approximated by the normal distribution,
due to the Central Limit Theorem (CLT), which states that as the sample size increases, the distribution of the sample mean tends toward the normal, irrespective of the shape of the original (parent) population. In addition, the distribution of the sample mean has a smaller spread, or variance, compared to the original distribution (due to the effects of averaging).
Application
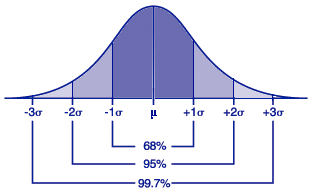
The Empirical Rule or 68-95-99.7% Rule states that 68% of the values under the normal curve fall within one standard deviation of the mean, 95% within two standard deviations and 99.7% within three standard deviations of the mean. This rule holds for all normal distributions (with any mean and standard deviation) and helps estimate normal probabilities.