Definition

A very useful property of fractional Factorial Designs, in which a single replicate of a design with several Factors, contains within itself one or more Replicates of a full factorial design in any subset of Factors. Thus, if you have a fractional design of resolution R and only (R-1) of them are significant, then the resolution R design will contain one replicate of a full factorial design in the (R-1) significant Factors. This property is also known as ‘Hidden Replication’.

In general, a resolution R fractional design contains 1 replicate of a full factorial design in any subset of (R-1) Factors, 2 Replicates of a full factorial in any subset of (R-2) Factors, 3 Replicates of a full factorial in any subset of (R-3) Factors and so on. This property is especially useful in the screening stage of an experiment, when there are a large number of potential Factors of which only a few are actually expected to have large effects.

Examples

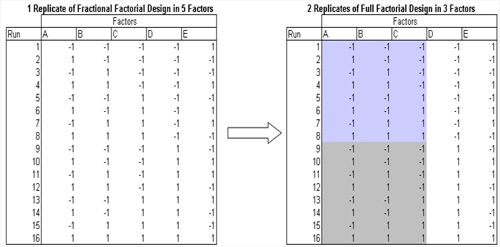
Consider a half fractional design of five factors – this is a resolution V design. Suppose three of these factors, A, B and C, are found to be significant. The half fraction can now be projected into two replicates of a full factorial in the three factors, as shown in the graphic alongside. This will allow you to obtain an independent estimate of the experimental error, in addition to more precise effect estimates for the three factors and their interactions.