Definition
Also called the coefficient of determination, R2 measures the relative amount of variation in the response ‘Y’ that is explained/accounted for by changes in the predictor variable ‘X’. In the case of several predictors, R2 represents the proportion of the variation in Y accounted for by the regression model or the specific combination of the set of predictors.
R2 takes values between 0 (zero) and 1, with larger values being more desirable. It is often used to evaluate the fit of the regression model to the data – higher the R2 value, better the fit.
In the case of a single dependent variable (Y) and a single independent variable (X), R2 is simply the squared correlation coefficient between X and Y. In the case of several X's however, R2 has a disadvantage, because it does not take into account the number of variables already in the model. Thus, its value increases as the number of variables in the model increases, even if those variables are not statistically significant. This shortcoming is corrected by using the related statistic called Adjusted R2.
Examples
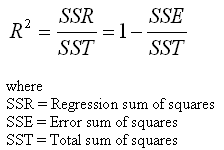
See Also
R-Squared (Adjusted)
