Definition
The Paired t-test is used to determine whether a significant difference exists between two related Populations. The related Populations have some characteristic in common, such as observations on the same items/subjects or items that are more similar than the general population. This removes the extra source of variation among the items and provides a level ground for the evaluation of the factor of interest. If the paired-data assumption is valid, the paired t-test is more powerful than the test based on the assumption that the observations are independent.
Examples
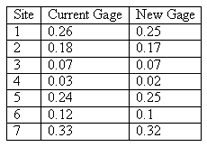
A weather service bureau is conducting a study to evaluate a new all-weather precipitation gage to find a possible replacement for the current gage. The two gages are used to measure precipitation at six test sites and the difference between each reading and the reference value (obtained from a standard gage from a national body) is recorded.
The readings from the two gages are related by site, so this dataset should be analyzed with a paired t-test. The test is basically a one-sample t-test performed on the differences of the observations from the two samples. The null hypothesis is H0 : µcurrent-newd = 0, against the alternative H1: µcurrent-new > 0.
The standard deviation of the differences is 0.0095. The pooled estimate using the individual sample standard deviations is 0.1093. The paired t-test gives a p-value = 0.047. The independent samples t-test with a pooled estimate of the standard deviation, gives a p-value = 0.452. The test is significant at the 5% level in the first instance but not in the second.
