Definition
The main effect of a predictor/independent variable is defined as the change in the output/response variable as a result of changing from the low to the high level of the predictor variable, averaged over all the other predictor variables in the experiment.
Examples
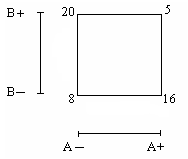
Consider a simplified example of a single replicate of a factorial experiment with two factors A and B, each at two levels. The diagram shows the design space with the four factor-level combinations. The vertices of the square show the corresponding response values.
The change in the response variable going from the high (A+) to low (A-) level of A is 5-20 = -15 at the high level of B (B+) and is 16-8 = 8 at the low level of B (B-). Thus the average change in the response is = (-15 + 8)/2 = -7/2 = -3.5. Thus the main effect of factor A is 3.5 in the negative direction (high levels of A lead to lower response values).
The same computation may be made using another formula: Main effect A = 1/2*[(total response at A+) - (total response at A-)] The total at (A+) is 5+16 = 21. The total response at A- is 20+8 = 28. The main effect of A is then given by: 1/2*(21-28) = -7/2 = -3.5.
External Links
More on Main Effect: - http://davidmlane.com/hyperstat/A131633.html
