Definition

The Poisson probability distribution describes the number of occurrences of an event in a fixed amount of time, such as number of patients arriving at an emergency room in a half-hour interval. The definition of 'event' also extends to non-temporal events, such as the number of Defects in a yard of cloth or the number of pot-holes in a square mile area.
The conditions or assumptions required to be satisfied for a variable to have a Poisson distribution are:
1. The average number of events during the specified interval is constant.
2. The occurrences of the event are independent
The distribution has one parameter: λ.
The mean and variance are both equal to λ.
Examples
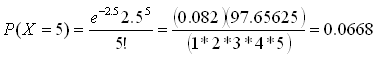
A call center switchboard gets 2.5 calls per minute on average. What is the probability that in a given minute, the switchboard receives exactly five calls?
Application
The poisson distribution can be used to approximate the binomial distribution when n is large (> 30) and p is small, such that the binomial mean, np, is less than or equal to 7. In this case, the mean of the binomial becomes the poisson mean lambda, i.e., np = λ.
External Links
More on the Poisson Distribution from NIST: - http://www.itl.nist.gov/div898/handbook/eda/section3/eda366j.htm
