Definition
Center points are used to detect curvature (non-linearity) in the factor effects and to provide an internal estimate of the error variance in a two-level factorial design. If the experimental design involves only continuous Factors, then center points are added as replicated runs at the center of the design (where the mid-points of the factor Ranges intersect). If one or more attribute Factors are involved, then these Replicates include the high and low levels of the attribute Factors. In unreplicated designs, center points are used to obtain a measure of the error without sacrificing higher order effects.
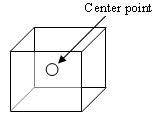
The figure alongside shows a three factor design (represented by the cube) including a center point.
Application
If each factor in the design is studied at its 'low' and 'high' levels (in coded units: x = -1 and x = +1), the center points consist of running replicates at the points where each factor is at its midpoint, (in coded units, x = 0). Center points only help to test for curvature. If Curvature is detected, it implies the need for quadratic terms of the form x2 in the model equation. However, axial points will be needed to estimate these quadratic effects.
External Links
Adding Center Points to a Factorial Design: - http://www.itl.nist.gov/div898/handbook/pri/section3/pri337.htm
